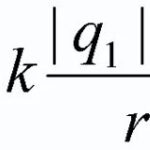什麼是電位和兩點之間的電位差

電勢的概念是靜電學和電動力學理論的重要基礎之一。了解其本質是進一步研究這些物理學分支的必要條件。

什麼是電勢

讓單位電荷 q 放置在由固定電荷 Q 創建的場中，該場受以下因素影響 庫侖力 F=k*Qq/r。

此處及以下 k=((1/4)*π* ε* ε)，其中 ε_{0 —} 電常數（8.85*10^-12 F/m)，而 ε 是 介質介電常數.

貢獻了 收費 在這個力的作用下，它可以移動，這個力會做一定的功。這意味著由兩個電荷組成的系統的勢能取決於兩個電荷的大小和它們之間的距離，而這個勢能的大小不取決於電荷 q 的大小。這裡引入了電勢的定義——它等於場的勢能與電荷大小的比值：

φ=W/q，

其中W是由電荷系統產生的場的勢能，勢是場的能量特徵。為了使電荷 q 在電場中移動一段距離，需要花費一定的功來克服庫侖力。一個點的電勢等於將一個單位電荷從該點移動到無窮遠所必須消耗的功。在此過程中，應注意：

• 這個功等於電荷勢能的減少（A=W₂-W₁);
• 功不取決於電荷的軌跡。

在 SI 系統中，電勢的單位是一伏（在俄羅斯文獻中用字母 V 表示，在外國文獻中用字母 V 表示）。 1 V \u003d 1J / 1 C，即我們可以談論1伏點的電勢，如果需要1焦耳將1 C的電荷移動到無窮大。這個名字是為了紀念意大利物理學家亞歷山德羅·沃爾塔，他為電氣工程的發展做出了重大貢獻。

為了可視化電位是什麼，可以將其與兩個物體的溫度或在空間中不同點測量的溫度進行比較。溫度是物體加熱的量度，電勢是電荷量的量度。據說一個物體比另一個物體受熱更多，也可以說一個物體帶電多，另一個物體帶電少。這些機構具有不同的潛力。

勢的值取決於坐標系的選擇，因此需要一定的水平，必須取為零。例如，在測量溫度時，可以將融冰的溫度作為基線。對於電位，通常將無限遠點的電位視為零電平，但為了解決一些問題，例如，可以將地電位或其中一個電容器極板的電位視為零。

潛在屬性

在電位的重要性質中，應注意以下幾點：

• 如果該場由多個電荷產生，則特定點的電勢將等於每個電荷產生的電勢的代數（考慮電荷的符號）總和 φ=φ₁+φ₂+φ₃+φ₄+φ₅+…+φ_n;
• 如果與電荷的距離使得電荷本身可以被認為是點電荷，那麼總勢由公式 φ=k*(q₁/r₁+q₂/r₂+q₃/r₃+…+q_n/r_n)，其中 r 是與所考慮點的相應電荷 then 的距離。

如果該場由電偶極子（符號相反的兩個相連的電荷）形成，那麼距離偶極子距離為 r 的任何點的電勢將等於 φ=k*p*cosά/r²， 在哪裡：

• p 是偶極子的電臂，等於 q*l，其中 l 是電荷之間的距離；
• r 是到偶極子的距離；
• ά 是偶極臂與半徑矢量 r 之間的角度。

如果該點位於偶極子的軸上，則 cosά=1 且 φ=k*p/r².

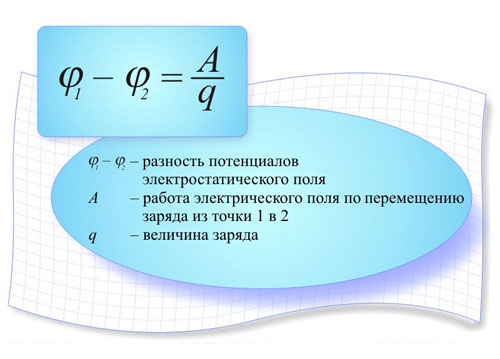
潛在差異

如果兩點具有一定的電位，如果不相等，則稱兩點之間存在電位差。點之間出現電位差：

• 其潛力由不同符號的電荷決定；
• 一個具有來自任何符號電荷的電位的點和一個具有零電位的點；
• 具有相同符號勢但絕對值不同的點。

也就是說，電位差不取決於坐標系的選擇。可以用相對於零標記（例如海平面）位於不同高度的水池進行類比。

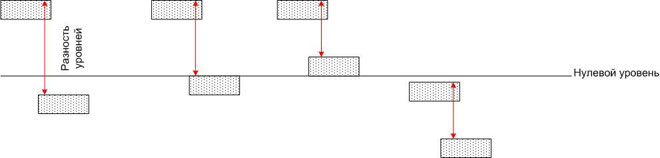
每個水池的水都有一定的勢能，但是如果你用一根管子把任意兩個水池連接起來，那麼每個水池裡都會有水流，水流的流速不僅取決於管子的大小，還取決於地球引力場中的勢能差異（即高度差）。在這種情況下，勢能的絕對值無關緊要。

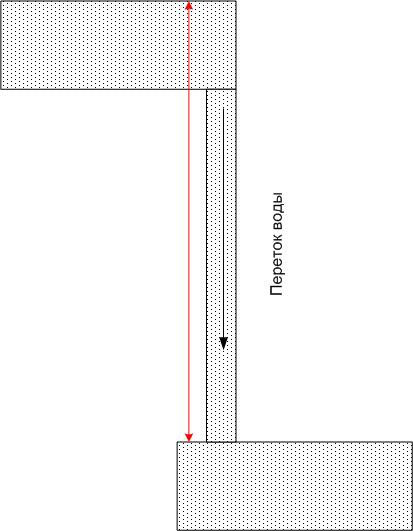
同理，如果用導體連接兩個電位不同的點，它就會流動 電，不僅取決於導體的電阻，還取決於電位差（而不是它們的絕對值）。繼續以水進行類比，我們可以說上層水池中的水很快就會用完，如果沒有力量將水向上移動（例如泵），那麼水流將很快停止。

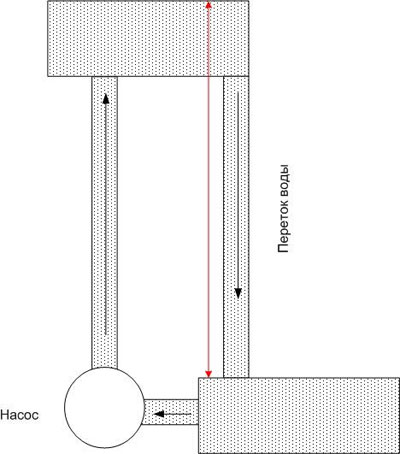
所以它在電路中 - 為了將電位差保持在一定水平，需要一種力將電荷（更準確地說，電荷載流子）轉移到具有最高電位的點。這種力稱為電動勢，縮寫為 EMF。 EMF 可以具有不同的性質——電化學、電磁等。

在實踐中，重要的是電荷載流子軌蹟的起點和終點之間的電位差。在這種情況下，這種差異稱為電壓，在國際單位制中，它也以伏特為單位。如果將1庫侖的電荷從一個點移動到另一個點時，如果場做1焦耳的功，我們可以說1伏特的電壓，即1V \u003d 1J / 1C，而J / C也可以是單位潛在差異。

等電位面

如果幾個點的電位相同，並且這些點形成一個面，那麼這樣的面稱為等勢面。例如，這種性質具有圍繞電荷的球體，因為電場在所有方向上均等地隨著距離而減小。

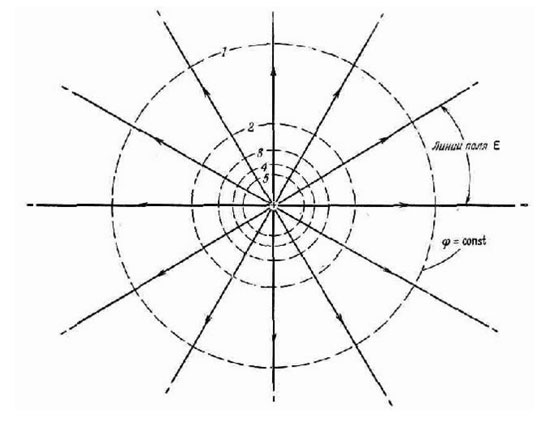
這個表面的所有點都具有相同的勢能，因此當在這樣的球體上移動電荷時，不會消耗任何功。多個電荷系統的等勢面具有更複雜的形狀，但它們有一個有趣的特性——它們從不相交。電場的力線總是垂直於在每個點處具有相同電位的表面。如果等電位面被一個平面切割，將得到一條等電位線。它具有與等勢面相同的性質。例如，在實踐中，放置在靜電場中的導體表面上的點具有相等的電位。

處理完電位和電位差的概念後，您可以繼續進一步研究電現象。但不是更早，因為不了解基本原理和概念，就不可能加深知識。

類似文章：